Educational Systems Theory

Property: System

Definition:

"A system is a group with at least one affect relation which has information." (p. 44)

Illustration:

Comments:

1. Universe of discourse

1.1. This is a primitive term. Primitive terms are undefined. Otherwise, circularity would be introduced into a definition system. The universe of discourse is whatever the inquirer deems it to be -- i.e., all that is relevant to the problem at hand. With regard to education, the universe of discourse would include education systems and their surroundings, communities, states and nations, depending on where one wants to draw the line.

2. Component

2.1. This too is a primitive term. Components of the universe of discourse in education could include people, living and non-living things, places, events; iconic representations of people, living and non-living things, places and events (e.g., pictorial illustrations, film, video and audio recordings, computer graphics); and abstract representations of these entities (e.g., words and numbers in books, periodicals, and computers).

3. Group

3.1. "A group is at least two components that form a unit within the universe of discourse." (p. 40)

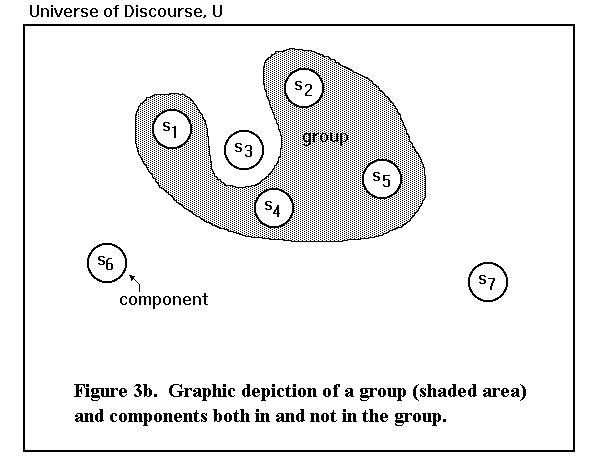
3.2. Analogous terms in set theory are 'set', 'elements', and the 'universal set'. In Figure 3b, Components s1, s4, s2 and s5 form a group. components s6, s3 and s7 are not in the group.

Illustration:

4. Characterization

4.1. This is a primitive term.

4.2. We can characterize things in many ways, normally by using 'signs' to refer to things, persons, places, events, etc. 'Signs' can be symbolic/abstract such as spoken or written words, but can also be icons, gestures, facial expressions, mime, demonstration by enactment, touch, etc. Some signs we use in education are 'teacher' (for one who guides the learning of another) and 'student' (for one who is attempting to learn).

5. Information

5.1. "Information is a characterization of occurrences." (p. 40)

5.2. The notion of information is very specific here. "'information', 'I', equals by definition 'characterization, CH, such that CH is equal to a set of categories, c, such that that probability distribution, p, such that the pair of c and the real number, v, (c,v), is an element of p'." (p. 40)

5.3. For example, suppose we have four categories of roles in education: teacher, student, administrator, and staff. Suppose in some education system we have 9 teachers, 11 administrators (parent volunteers, serving as a board of directors), 2 staff members and 150 students (total of 172 persons). We can compute relative frequencies to estimate the probability distribution of person-roles: p(teacher)= 9/172 = .05; p(administrator) = 11/172 = .06; p(staff) = 2/172 = .01; p(student) = 150/172 = .87.

5-1. Selective Information

5-1.1. "Selective information is information which has alternatives." (p. 40)

5-1.2. This means that there is uncertainty. Thus, there must be at least one category which has a probability that is not equal to zero or one. In the above example, this is true. The information about the set of person roles is {(teacher,.05), (administrator,.06), (staff,.01), (student,.87)}. There is uncertainty in the probability distribution. If we were to visit this school, the most likely person we would observe is a student. However, we will occasionally meet others such as teachers and parent board members. On the other hand, if every person was a student (probability = 1.0), then there is no selective information -- no uncertainty of category occurrences.

We can measure degree of uncertainty in a probability distribution with H, from information theory. H is maximum when categories are equiprobable. H is minimum when one category has a probability of occurrence of one and all others zero.

5-1-1. Nonconditional Selective Information

5-1-1.1. "Nonconditional selective information is selective information which does not depend on other selective information." (p. 41)

5-1-1.2. This is akin to the notion of independence in probability theory. Suppose we have two classifications: Person's Role and Ethnicity. Suppose our categories of ethnicity are: African-American, Anglo, Asian, Hispanic and Other. We could obtain a distribution of persons according to their ethnicity. If the p(Hispanic) = a, if the p(administrator) = b, if the p(Hispanic and administrator) = a b, and if this is true of all pairs of roles ethnicity, then we would say that the two probability distributions are independent. In other words, the role taken by a person does not depend on his or her ethnicity.

For example, the probability of being an Hispanic person and an administrator is 0.20 x 0.06, which is equal to 0.012. The same is true for African Americans.

5-1-2. Conditional Selective Information

5-1-2.1. "Conditional selective information is selective information which depends on other selective information." (p. 41)

5-1-2.2. In this case there is a statistical dependence. Each cell probability is no longer equal to the product of its marginal probabilities, as it is for nonconditional selective information. Notice for example, if all administrators are Anglo, then no administrators are from African-American, Asian, Hispanic or Other ethnic backgrounds.

Note that here the probability of being and African-American and an administrator is 0.000 (not 0.012 as above for nonconditional selective information). If you are an African-American in this example, you are not going to serve in the role of administrator. This is conditional selective information.

6. Transmission of Selective Information

6.1. "Transmission of selective information is a flow of selective information." (p. 42)

7. Affect Relation

7.1. "An affect relation is a connection of one or more components to one or more other components." (p. 42) In the below figure the affect relations are (s7,s6), (s1,s4), (s1,s2), (s1,s5), (s4,s2), (s4,s5), (s2,s5), (s5,s2),

Illustration:

7-1. Directed Affect Relation

7-1.1. "A directed affect relation is an affect relation in which one or more components have a channel to one or more other components." (p. 43)

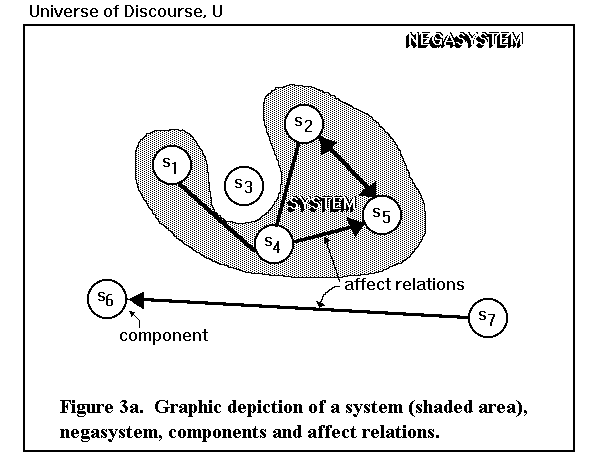
7-1.2. In the above figure directed affect relations exist between (s7,s6), (s4,s5), (s4,s2), (s2,s5), and (s5,s2).

7-1-1. Direct Directed Affect Relation

7-1-1.1. "A direct directed affect relation is a directed affect relation in which the channel is through no other components." (p. 43)

7-1-1.2. In the above figure the direct directed affect relations are: (s7,s6), (s4,s5), (s2,s5), and (s5,s2).

7-1-2. Indirect Directed Affect Relation

7-1-2.1. "An indirect directed affect relation is a directed affect relation in which the channel is through other components." (p. 44)

7-1-2.2. In the above figure, the indirect directed affect relation is (s4,s2). The channel is through s5.

Go to SIGGS Home Page.